Numerical simulation of sediment transport by thermohaline bottom currents
Ocean Sciences, Computational fluid dynamics
Research area
This project is focused on the study of the sediment transport and deposition mechanisms on the sea bottom.
In particular, it concerns the interaction between two types of currents flowing on the sea floor: turbidity (downslope) and contour (along slope) flows.
Turbidity flows are dense currents where mixtures of sediment and water travel downslope because they are denser than the surrounding water.
The contour currents are driven by thermohaline density gradients and forced by the Coriolis effect to travel along the continental slope within the geostrophic oceanic currents.
Project goals
The aim of this study is to use numerical simulations to reproduce the effect of this interaction on the solid transport, in order to improve its comprehension.
Indeed, the processes described above are controlling critical deep-sea aspects including seafloor habitats, slope instability, microplastic distribution, hydrocarbon reservoirs.
Computational approach
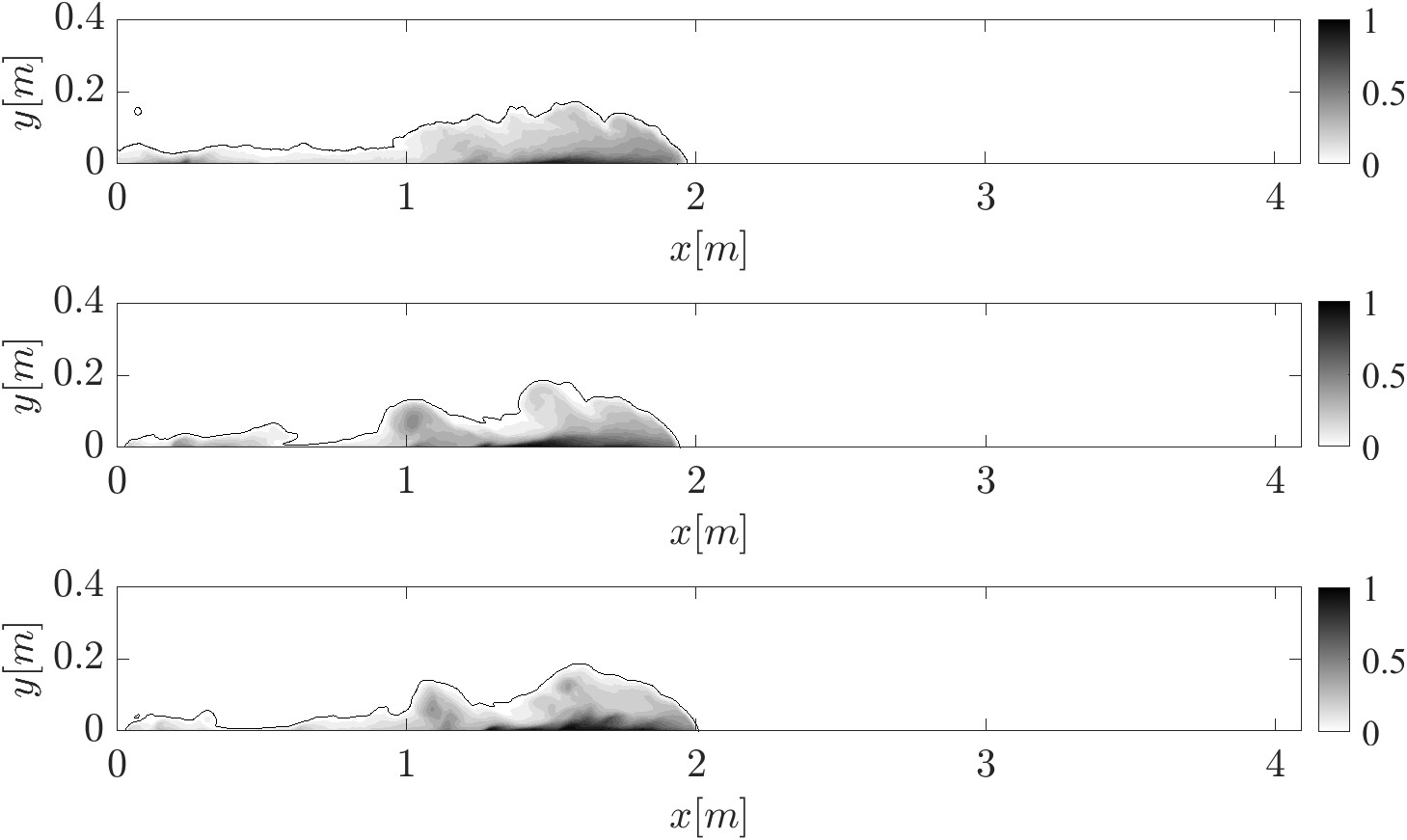
The numerical approach is based on the Large eddy Simulations, so on the filtered Navier Stokes Equation, to which was added a salinity/sediment transport equation. To extend affordable case studies to higher Reynolds numbers, averaged approaches can be used. The URANS method reduces computational costs by averaging the Navier-Stokes equations over time, but at the expense of accuracy. A better compromise is LES, which directly resolves larger turbulent structures while modeling smaller dissipative scales. However, near-wall regions remain challenging, as resolving them requires DNS-level mesh resolution, making high-Re simulations computationally expensive. To address this, WF-LES combines LES with Wall Functions, which model near-wall turbulence effects without requiring fine mesh resolution. This method assumes that the first computational cell near the wall contains multiple eddies, allowing an averaged approach similar to RANS. Using Wall Functions significantly reduces computational costs while maintaining reasonable accuracy. In some cases, mesh resolution requirements can be reduced by an order of magnitude, from 10^7 to 10^6 cells. So the first step is to validate this approach and then study cases with Reynolds number next to the real scale phenomenon.
Density fields, a confrontation between a fully resolved LES simulation (top) and two WF-LES (center and bottom).
Antonio Ammendola
University of Trieste; OGS
Antonio Ammendola is an environmental and civil engineer specializing in computational fluid dynamics, microclimatic monitoring, and numerical modeling. He holds a Master’s degree in Environmental Engineering from the University of Trieste and a Bachelor’s in Civil Engineering from the University of Reggio Calabria. Currently, he is a PhD candidate at the University of Trieste, researching sediment transport in thermoaline bottom currents. Previously, he worked as a research fellow at Politecnico di Milano, focusing on environmental monitoring of cultural heritage and CFD modeling of convective flows. He has also gained experience in energy efficiency analysis and hydraulic device testing. Antonio has organized academic workshops and holds certifications in workplace safety and English (C1). His technical skills include OpenFOAM, ANSYS Fluent and statistical analysis. His research interests cover computational and environmental fluid dynamics, with several publications in these fields.