Research area

Vegetation patterns are a common feature of dryland ecosystems. The most frequently observed types are gaps, stripes/labyrinths and dots patterns, with a defined spatial scale, but irregular and scale-free patterns have also been recognized.
Various explanations have been provided for this phenomenon, our working hypothesis is that of vegetation self-organization. In arid and semi-arid ecosystems, several positive feedbacks encourage vegetation growth in the short range.
Concurrently, the different vegetation units compete for the limited water resource over a longer range.
The sum of these two mechanisms produces an instability to heterogeneous disturbances in the uniform vegetation solution at a certain precipitation value, below which the system falls into a stable patterned state.
The possibility to form patterned states improves the recovery capacity of the ecosystem since it breaks the large hysteresis cycle between desert and uniform vegetation solutions.

Project goals

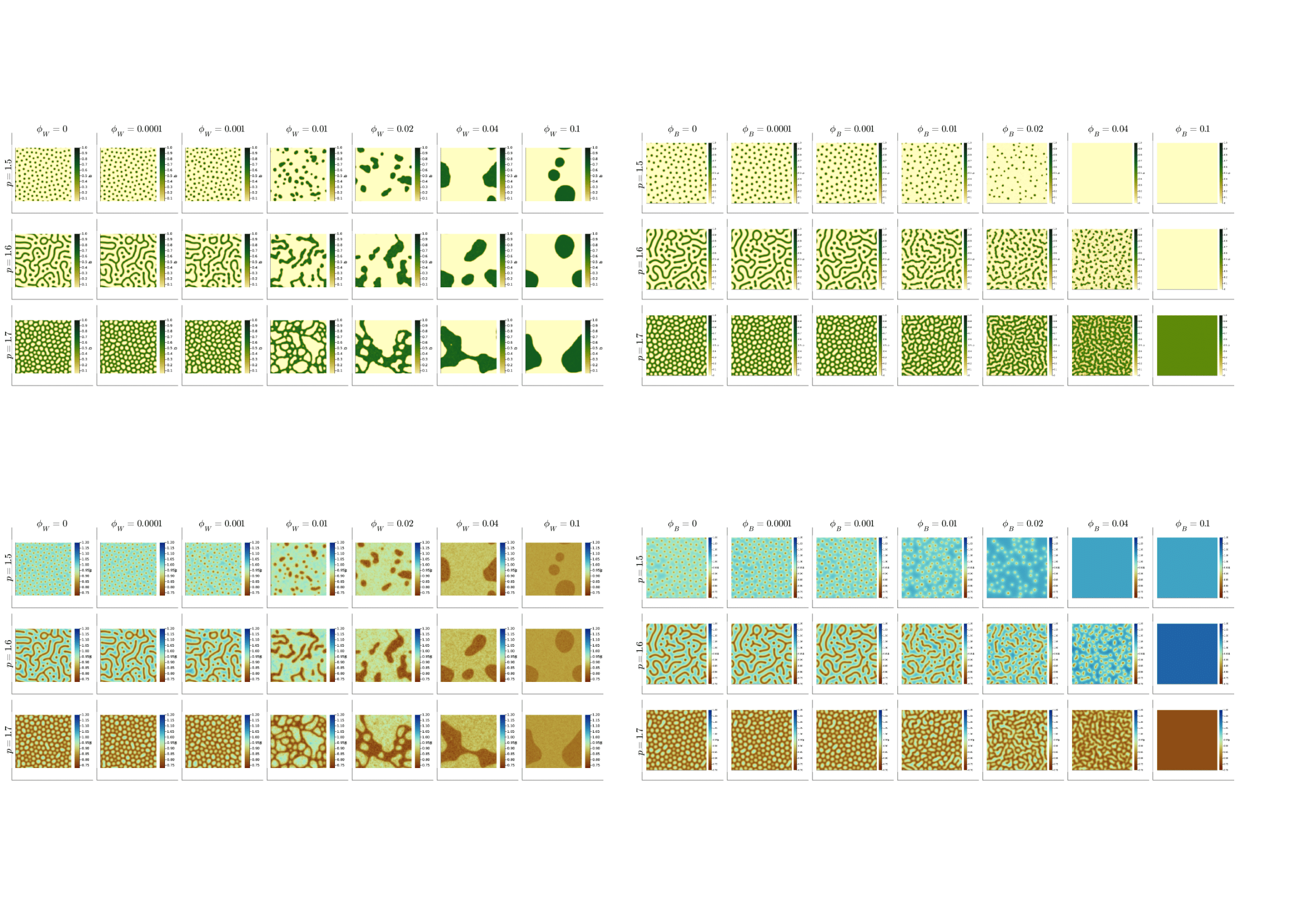
In our project we investigate the effects of non-local connections on the process of pattern formation. Our starting point is a two-equation reaction-diffusion model, describing the dynamics of water and biomass densities in a 2-dimensional space. We modify the diffusive terms of this model to operate in a network space: each point in the spatial 2D grid represents a node in the network, and resources (water or biomass) diffuse from it to all its linked nodes. Following the Watts-Strogatz small world network model, starting from the 2D lattice, we draw shortcuts between a certain number of random nodes, preserving the original lattice links in the process. The number of shortcuts becomes a model parameter describing the topology of the diffusion network. We develop two different cases.

1. Case 1: water diffuses through shortcuts, while biomass diffuses on the regular grid.
2. Case 2: biomass diffuses through the shortcuts and water on the regular grid.

We study the sensitivity of the model to this parameter and evaluate how the stable pattern states change when they form over a different network topology. We believe our study may help explain the formation process of irregular and scale-free patterns, and predict their behaviour in front of changing environmental conditions.

Computational approach

At present, the model is implemented in Julia code. We employ the ParallelStencil.jl package, which allows us to solve the two model equations in parallel, greatly reducing the computational times and providing good efficiency and scaling.
Currently we are using a limited number of CPUs for each experiment (4/8)  but we intend to perform a wider exploration of the parameters space, using large ensembles of simulations in parallel in order to estimate uncertainties.
To this end, in-house computational resources would not suffice and we are looking forward to use additional resources in the project to this end.
Further, simulations over larger domains would be useful to evaluate possible long distance ordering of our patterns but would require additional computing resources.
For this last purpose, we are interested in experimenting with the use of GPUs (for which our code is already ready thanks to the ParallelStencil.jl implementation), to improve scaling over larger domains.

Key results

XXXXXXXXXXXXXXXXXX

Resource usage

In our model, we study the impacts on pattern formation of the topologies of biomass and water diffusion networks, controlled by the hyper-parameters ϕ_b and ϕ_w, respectively. In our previous study, these two factors were considered separately, by always setting one of the diffusion networks to a regular grid and gradually modifying the other. We used the TeRABIT resources to extend our work and analyze the full parameter space, accounting for the interactions between complex biomass and water diffusion networks. This allowed us to uncover several new properties of our system. For instance, we found that broad patch size distribution patterns (with an exponential distribution of patch sizes) emerge over a wide range of topologies, rather than only in a short range of the parameter ϕ_w , as previously assumed. Finally, we used the TeRABIT resources to strengthen our previous results by more extensive statistics.

What's next

Presently, we are continuing the analysis of the simulations produced thanks to the use of previously assigned TeRABIT resources. These concern the interaction between water and biomass diffusion networks in our model and their comprehensive impact on pattern formation. We hope these analysis will coalesce into a publication in the near future. Concomitantly, we are working on our contribution to a wider project concerning the capacity of living systems to avoid tipping points through adaptation mechanisms such as pattern formation. We will be focusing on the effect of short term droughts in our model. In particular, we wish to study the limits to our system's ability to recover from a disturbance, depending on its temporal scale and intensity. For this topic, we plan on exploiting the HPC Bubble resources at INFN Torino, as of agreements following the final TeRABIT workshop. Finally, a possible future research line may emerge from considering the topology of the biomass diffusion network as a functional trait of the plant species (reproduction mechanism), and studying the evolutionary dynamics connected to this trait. Resources to be used for this last line of inquiry are to determined.